Physics Overview
Quarks are the most fundamental constituents of matter discovered so far. Their interaction via the strong force is key to their behaviour because this force prevents them appearing as free particles and means that we must study them through experimental observation of their bound states known as hadrons. Examples of hadrons are the protons and neutrons that make up the atomic nucleus. The collision at high energy of particles (such as protons) then does not liberate the proton’s quark constituents but instead converts the energy of the collision into showers of further hadrons. The hadrons can be tracked in particle detectors and properties, such as their mass, determined. These properties reflect those of their quark constituents and their behaviour under strong force interactions and so can be predicted if we can solve the theory.
Quantum Chromodynamics (QCD) is the theory that describes the strong force, through the interaction of quarks carrying colour charge via force carriers called gluons. QCD operates in a similar way to Quantum Electrodynamics (QED) that describes electromagnetism but unlike the force carriers of QED (the photon) the gluon also has colour charge and this produces very different physics. Gluon self-interactions cause an anti-screening of quark colour charge so that, for example, the effective strength of the quark-antiquark interaction (denoted by the strong coupling constant, $\alpha_s$) increases with their separation. This leads to the phenomenon of quark confinement mentioned above. The strongly-coupled non-linear behaviour of QCD (necessary to produce confinement) means that it has to be solved numerically to determine hadron properties. This is recognised as one of the “Grand Challenge” problems of computational physics.

Lattice QCD provides a framework for the numerical calculation in which the theory is discretised onto a lattice of space-time points. Very fast supercomputers are required to perform the calculations. Pictured is one of the computers that we use, Darwin at the Cambridge High Performance Computing Service which is part of the UK Science and Technology Facilities Council’s DiRAC High Performance Computing facility.
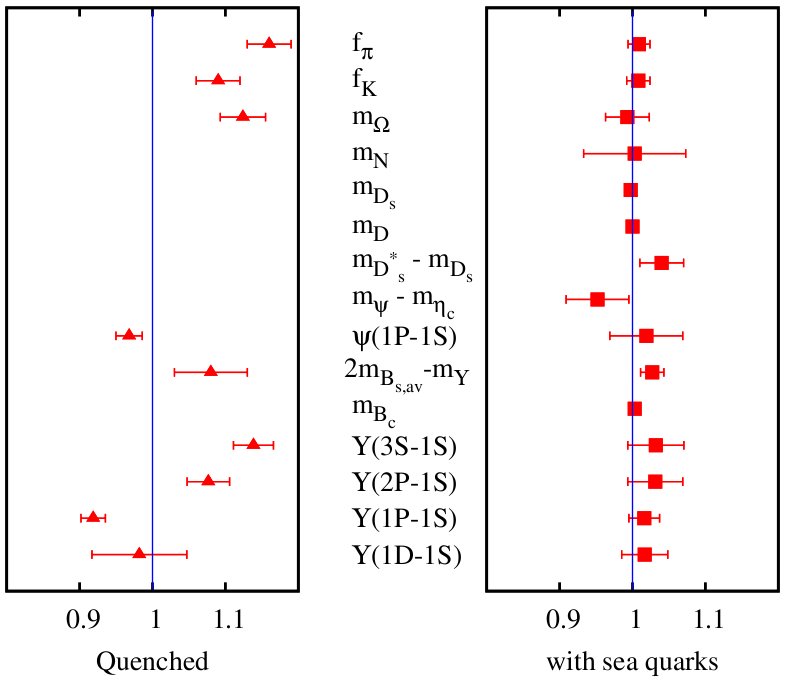
HPQCD has been at the forefront of progress in lattice QCD that has led to its recognition as a precision tool for phenomenology. It is critical for this that we include in our calculations the effect of quantum energy fluctuations that create quark-antiquark pairs (sea quarks) to give a realistic picture of the background strongly-interacting ‘soup’ in which the valence quarks that make up the hadron live. In 2003 together with the MILC and Fermilab Lattice Collaborations we showed that including the effect of sea quarks does indeed make a dramatic difference in the agreement of lattice QCD results with experiment (C. T. H. Davies et al, Physical Review Letters 92:022001 (2004), arXiv;hep-lat/0304004). Below we show an updated version of the ‘ratio plot’ in which ratios of lattice QCD results to experiment are shown for a wide variety of quantities from pi and K meson annihilation amplitudes through baryon masses to mass differences among Upsilon mesons. On the left sea quarks are missing; on the right a realistic complement of sea quarks is included.
Since then we have developed many improved techniques for the determination of hadron masses and the rate of their weak and electromagnetic decay processes for comparison to experiment. For example, a particularly numerically efficient and accurate method for handling quarks on a space-time lattice is our Highly Improved Staggered Quark (HISQ) formalism. These methods have enabled stringent tests of QCD and allowed the accurate determination of quark masses, the strong coupling constant and the Cabibbo-Kobayashi-Maskawa matrix elements that couple different types of quarks to the W-boson of the weak force.
Further reading:
-
Joining the dots with the strong force,
Cover feature in CERN Courier, June 2004. - Colourful calculations,
Physics World, December 2006